Introdução ao Teorema de Bayes
Você já ouviu falar sobre o Teorema de Bayes ou como ele pode ser aplicado?
Se você não conhece a probabilidade estatística, provavelmente ainda não ouviu falar nesse teorema, já que ele é um dos seus tipos.
Mas não é porque talvez nunca tenha ouvido falar sobre ele que isso signifique que sua criação é recente.

Na verdade, seu desenvolvimento ocorreu no século XVIII.
Thomas Bayes, matemático inglês e pastor protestante, foi quem o criou. Mas o que esse teorema tem a ver com um projeto Six Sigma?
Saiba que eles andam bem juntinhos já que quando um processo é estudado é preciso fazer uma estimativa da ocorrência de certo tipo de defeito.
Para poder calcular essa estimativa é preciso fazer uso da probabilidade.
Afinal, quando se estuda a probabilidade temos a oportunidade de determinar a ocorrência de um evento que esteja associado a um fenômeno.
Dentro dos projetos criados com o Six Sigma é preciso fazer o estudo da probabilidade para que os erros sejam reduzidos e os benefícios multiplicados.
Mas como é feita a distribuição estatística? O Teorema de Bayes pode realmente ajudar nesse sentido?
Como ele pode ser utilizado e para que serve? Tudo isso e muito mais veremos logo mais a seguir!
Tabela de Conteúdo
- Teorema de Bayes: o que é?
- Teorema de Bayes e o problema de Monty Hall
- Conclusão do Teorema de Bayes
Teorema de Bayes: o que é?
Dentro da matemática temos a probabilidade condicional cujo conceito envolve dois eventos e um espaço amostral que é finito e não vazio.
O Teorema de Bayes trata-se de uma fórmula matemática que é utilizada para calcular essa probabilidade.
Ou seja, ele vai determinar a probabilidade para que um evento aconteça em função de outro que já ocorreu.
Mas para que o Teorema de Bayes possa realizar esse cálculo é preciso que se tenha acesso a alguma informação anterior.
Essa inferência bayesiana deu início a uma expressão conhecida por “grau de crença“. Ela quer representar a confiança na suposição inicial que aquele evento anterior aconteceu.
Notação matemática do teorema da probabilidade condicionada
A notação matemática para a fórmula do Teorema de Bayes é:
P(A/B) = P(AB)/P(B)
Matematicamente, esses símbolos podem ser lidos da seguinte forma:
Probabilidade para A tal que B se iguala à probabilidade da ocorrência da intersecção entre A e B e divide-se pela probabilidade do B.
Mas o que significa esse “tal que”?
Ele quer dizer ser verdadeiro, ou seja, as chances reais que A aconteça com B sendo verdadeiro.
Assim, para que o P(A/B) seja atingido o B tem que ser verdadeiro.
Conheça a fórmula de Bayes e aprenda a calcular
Já sabemos que para calcular o Teorema de Bayes precisamos que um evento já tenha ocorrido para poder calcularmos outro dentro de um espaço amostral.
Vamos determinar esses eventos como A e B. Assim, a fórmula desse teorema será:
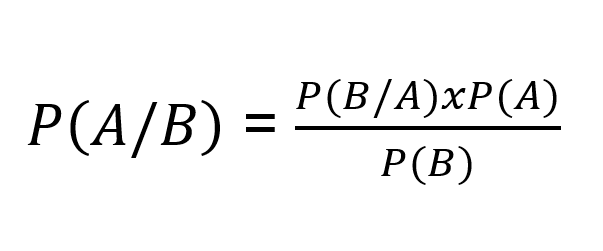
Vamos compreender o que significa cada um desses dados?
- P(B): probabilidade do evento B ocorrer
- P(A): probabilidade do evento A ocorrer
- P(B/A): probabilidade do evento B acontecer já que o evento A já ocorreu
Para a explicação ficar mais clara, que tal vermos um exemplo prático?
Exemplo Aplicado 1
Vamos imaginar que um casal tenha dois filhos e queremos saber a probabilidade das duas crianças serem do sexo masculino, sabendo que um deles é menino.
Antes de qualquer outra coisa, precisamos fazer a definição de alguns eventos e das probabilidades. Primeiramente, definiremos os eventos:
- A: os dois filhos são do sexo masculino (evento desejado)
- B: apenas um dos filhos é do sexo masculino (evento dado)
Agora que os eventos foram definidos, teremos que fazer a definição de algumas das probabilidades para então fazermos o cálculo:
- P(A): probabilidade para que os filhos sejam do sexo masculino
- P(B): probabilidade para que apenas um dos filhos seja menino
Se fizermos alguns cálculos simples concluímos que a probabilidade dos dois filhos serem meninos é de 1/4.
A probabilidade de uma das crianças ser menino é 1/2.
A partir daí, teremos que a probabilidade para que uma das crianças seja um menino é de 3/4.
Outra conclusão que podemos chegar é com relação a P(B/A). Nesse caso, a probabilidade de um dos filhos ser menino sabendo que os dois são do sexo masculino é 1.
A partir daí temos os seguintes dados:
- P(A) = 1/4
- P(B) = 3/4
- P(B/A) = 1
Ao aplicar esses dados na fórmula do Teorema de Bayes teremos:
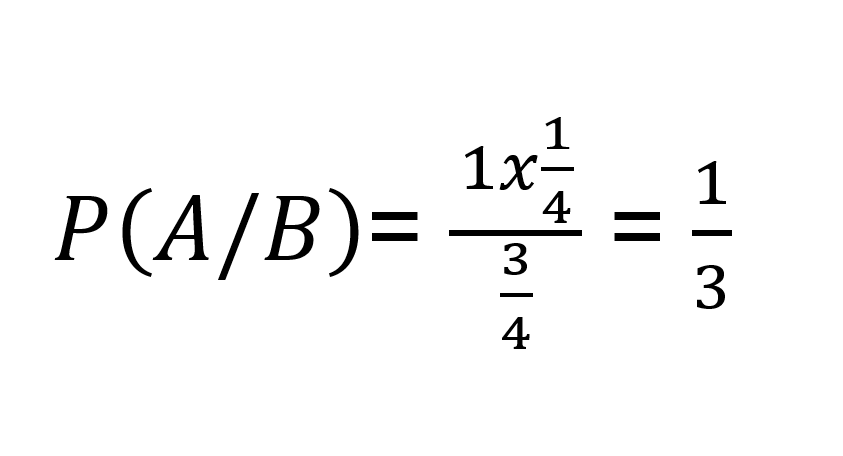
Conseguiu compreender como o Teorema de Bayes é calculado?
Esse foi um exemplo bem simples, mas e se colocarmos um mais completo?
Vamos ver como seria realizado o cálculo?
Primeiramente, saiba que o Teorema de Bayes pode ser aplicado em diversas situações e uma delas é a interpretação dos resultados dos testes de positividade de determinada doença.
Esses testes não possuem 100% de precisão e por esse motivo não é possível descrever os eventos reais com perfeição.
Agora que você já sabe disso, vamos elaborar nosso exemplo.
Exemplo Aplicado 2
Imagine que o teste de mamografia possui o seguinte comportamento:
- 9,6% das mamografias são capazes de detectar o câncer quando a doença não existe (ou seja, a porcentagem do resultado negativo dado corretamente é de 90,4%)
- 80% das mamografias acertam ao detectar o câncer quando a doença existe (sua margem de falha é de 20%)
- 1% das mulheres estão com o câncer de mama (quer dizer que 99% das mulheres não possuem essa doença)
Mas o que essas informações significam? De acordo com ela, dentre as mulheres que fazem esse exame, 9,6% delas têm chance de testarem positivo, enquanto que 90,4% irão testar negativo.
Das mulheres que têm câncer de mama, 80% testarão positivo para a doença, enquanto que 20% testarão negativo.
Dentre a população feminina, 1% das mulheres estão acometidas com esse tipo de câncer, enquanto que 99% não a possuem.
Agora que tivemos acesso a essas informações e a compreendemos, imaginemos que você ou alguém próximo a você fez a mamografia.
O resultado do teste foi positivo. Quais as reais chances desse resultado condizer com a realidade, ou seja, de realmente ter câncer?
Para chegarmos a essa resposta precisaremos calcular a probabilidade utilizando o Teorema de Bayes.
Vamos estabelecer os dados e fazer os cálculos:
- P(A) = probabilidade para ter o câncer (1%)
- P(B/A) = probabilidade do teste dar positivo (B) já que tem o câncer (A). A chance do positivo ser verdadeiro é 80%
- P(A/B) = probabilidade de ter a doença (A) sendo que o teste apresentou valor positivo (B)
- P(AC) = probabilidade da pessoa não ter a doença (99%)
- P(B/AC) = probabilidade do resultado do exame ser positivo (B) e a pessoa não ter a doença (AC) que corresponde a 9,6%
Utilizando a fórmula teremos:
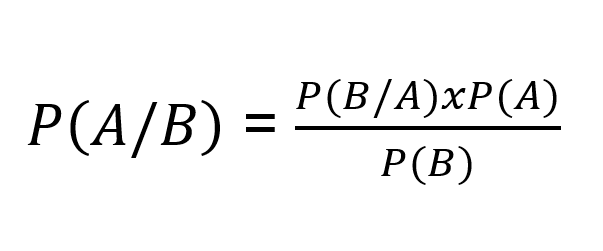
Para sabermos qual a probabilidade de um teste positivar precisamos conhecer todas as informações relacionadas ao teste dar positivo.
Por isso que fizemos toda a explicação dos dados.
Assim, percebemos que o teste pode dar positivo tanto em uma mulher que tenha câncer quanto na que não tem a doença.
Essas duas possibilidades correspondem a P(B/A) e P(B/AC). Dessa forma, teremos que P(B) será:
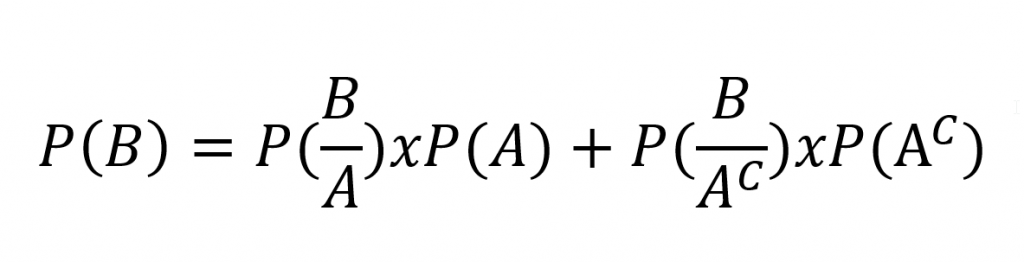
Ao jogar na fórmula do Teorema de Bayes temos:
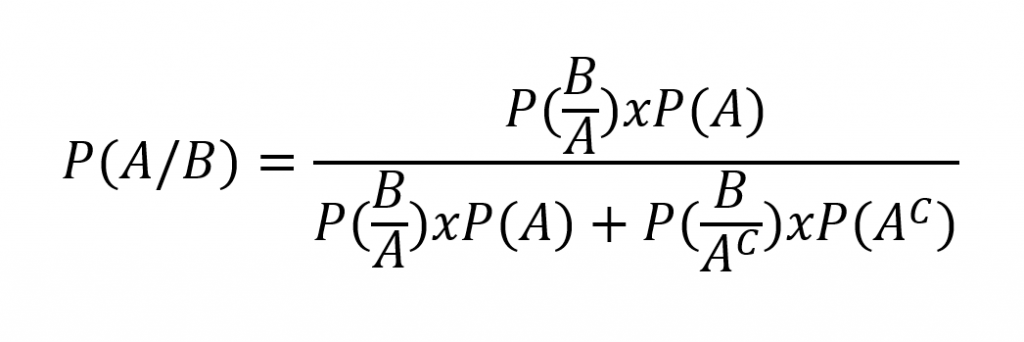
Substituindo pelos valores teremos:
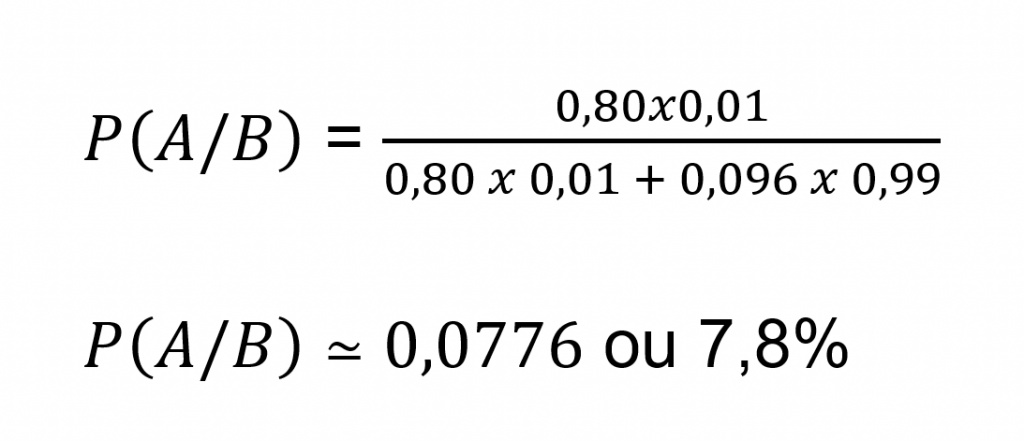
Isso quer dizer que a probabilidade da mulher está com câncer após a mamografia ter apresentado o resultado positivo é de 7,8%.
Para chegar a esse valor foi preciso fazer um cálculo com todas as possibilidades do teste dar positivo.
Teorema de Bayes e o problema de Monty Hall
Que tal pegarmos mais um exemplo para aplicar o Teorema Bayesiano?
Dessa vez, vamos utilizar algo que certamente você já viu em algum programa de TV, o problema do Monty Hall. Calma, o nome pode até ser a primeira vez que você entra em contato, mas a aplicação do problema não.
Sabe aqueles game shows que há uma quantidade de portas, apenas uma contém o prêmio e o convidado deve escolher a que ele acredita que é a premiada?
Pois bem, estamos diante do problema de Monty Hall e veremos como o Teorema de Bayes pode ser aplicado nesse caso.
Entendendo o princípio do problema
Este é um problema contra intuitivo e até controverso, mas com ele podemos determinar a probabilidade tendo como base o grau da crença.
No game show, o apresentador escolhe um participante que deve escolher uma das portas disponíveis no jogo.
Vamos dizer que temos três portas numeradas de 1 a 3.
Após dizer qual a escolhida, o apresentador pergunta se quer trocá-la.
Partindo do pressuposto que o apresentador sabe qual delas está o prêmio certamente ele vai abrir uma das outras duas que está vazia.
Em seguida, vai perguntar se deseja realizar a troca. Será que é uma boa ideia realizar a troca ou permanecer com a escolhida?
De antemão já comunico que ao optar pela troca, as chances de ser premiado dobram.
Vamos entender como a matemática consegue explicar isso?
Digamos que a porta escolhida foi a número 1 e o apresentador decide abrir a de número 2 que não contém nada.
Você deve lembrar que ele sabe em qual delas o prêmio se encontra. Ao abrir a porta e verificar que está vazia ele pergunta se deseja trocar.
Agora vamos aos dados referente a isso:
Ao escolher a porta número 1 as chances de ganhar são de 1/3, afinal, são 3 portas e somente uma é a premiada.
Quando o apresentador abre uma das portas as chances se mantêm as mesmas.
Definindo os eventos temos:
- A – a porta que foi escolhida (de número 1) é a premiada
- B – uma porta vazia é aberta pelo apresentador
Utilizando o Teorema de Bayes teremos:
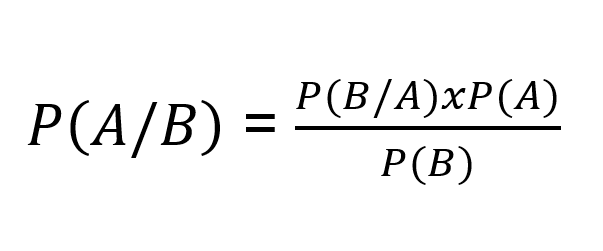
Já sabemos que o P(A) = 1/3 e que é preciso calcular P(B).
Para isso, todas as possibilidades existentes do apresentador realizar a abertura de uma porta vazia precisam ser cobertas.
Resumindo, é preciso determinar quais as chances de uma porta vazia ser aberta independente de uma delas ter sido ou não escolhida pelo convidado.
Dessa forma:
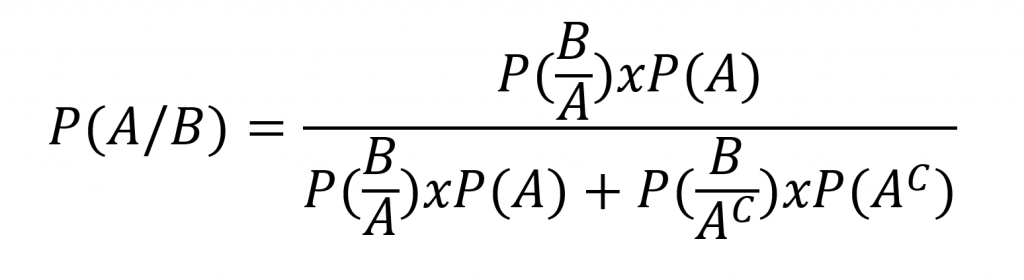
Definindo as probabilidades teremos:
- P(A) = probabilidade do prêmio estar na porta escolhida pelo convidado
- P(B/A) = probabilidade de uma porta vazia ser escolhida pelo apresentador supondo que a porta escolhida pelo convidado é a premiada
- P(A/B) = probabilidade de ter a doença (A) sendo que o teste apresentou valor positivo (B)
- P(AC) = probabilidade de a porta escolhida pelo convidado não ser a premiada
- P(B/AC) = probabilidade de uma porta vazia ser escolhida pelo apresentador supondo que o prêmio não se encontra na porta que o convidado escolheu
Assim, é possível afirmar que as chances do apresentador abrir uma das portas que está vazia, independente do prêmio estar ou não na porta escolhida, é igual a 1. Essa é a informação prévia.
Quanto a chance da porta errada ser escolhida, a probabilidade é de 2/3. Assim, se a primeira escolha for mantida a probabilidade de ganhar é:
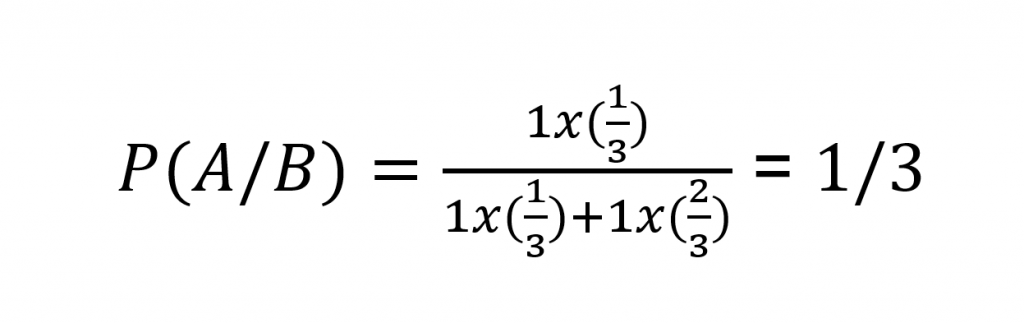
As chances de ganhar permanecem em 1/3. Mas se a troca for feita, as chances dobram para 2/3.
É claro que isso não garante que o prêmio seja ganho, afinal, a primeira porta escolhida pode ser a premiada. Mas não é incomum que a outra porta esteja com o prêmio.
Compreendeu o Teorema de Bayes?
Conseguiu compreender como que o Teorema de Bayes é utilizado e para qual finalidade?
A probabilidade se mostra muito importante em diversos setores e dentro de uma organização ela também pode mostrar sua face.
Quer se aprofundar mais nesse assunto? Então fique com a gente e adquira ainda mais conhecimentos!
